z-スコアの算出について
松田りえ子
国立医薬品食品衛生研究所安全情報部 客員研究員
JBCOの技能試験では、参加者のパフォーマンスをz-スコアを用いて評価しています。国立医薬品食品衛生研究所安全情報部 客員研究員
ここではその算出について解説します。
1. z-スコア
2. 平均値と標準偏差
3. 室間精度の予測とThompsonによるHorwitz式の修正式
4. ロバスト統計量(ロバスト平均値)
1. z-スコア
技能試験参加者の評価指標の一つとして、z-スコアがあります。z-スコアはある集団の中の相対的な位置を表す指標で、その集団が正規分布していることを前提としています。正規分布はFig. 1に示すような左右対称の分布で、中心(対称軸付近)が最も確率が高く、中心から離れるに従って確率が低くなるような確率分布です。正規分布は平均値と標準偏差の2つのパラメータだけで記述でき、平均値は分布の中心になります。標準偏差は分布の広がる範囲を表しますが、中心から中心+1標準偏差の範囲の確率は、中心や標準偏差が変わっても、常に一定であるという特徴があります。Fig. 1の平均値=0、標準偏差=1の正規分布は、標準正規分布と呼ばれます。
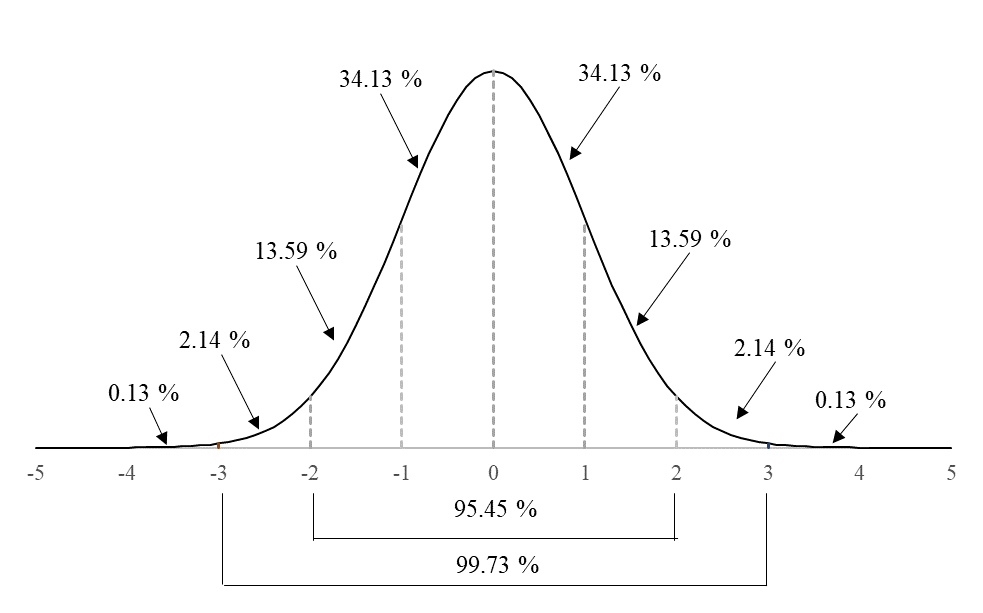
Fig. 1標準正規分布の確率密度
正規分布している確率変数 xi から分布の平均値 μ を引き、分布の標準偏差 σ で割ると、その変数が分布の中心から何標準偏差分離れているかが分かります。たとえばこの値が3であれば、Fig. 1の分布の一番右端に近い位置となり、分布の大部分の値よりも大きくなります。
z-スコアは下式で計算されます。
xi :参加者の報告値
µ :参加者の報告値の平均値
σ :標準偏差 このようにz-スコアは、分布の中の位置を示すことができます。また、Fig. 1に示すように、z-スコアが −2.0から2.0の範囲には分布の95.45 %が含まれますが、z-スコアの絶対値が3.0以上になるのは0.26 %であり、分布の中では少数であることがわかります。 z-スコアに10を掛け、50を足すと、偏差値が得られます。z-スコア=1は偏差値60、z-スコア=−2.0は偏差値30となります。異なる試験結果においても、偏差値が成績の比較に使用されるのと同様に、異なる技能試験での成績の比較あるいは傾向の分析にz-スコアを用いることができます。
技能試験の報告値はz-スコアに基づいて、以下のとおり評価されます(ISO/IEC 17043: 2023 B.4およびISO 13528:2022 9.4参照)。
| z-スコア | ≦ 2.0となる確率は、95.45 %とされておりその集団に属していると考えられるため満足とされます。
2.0 < | z-スコア | < 3.0となる確率は、約5 %でその集団に属する値であっても20回に1回程度はこの値となります。一方、その集団には属していないという可能性もあるため、疑わしいという評価となります。
| z-スコア | ≧ 3.0となる確率は、0.26 %とされており非常に小さくなります。その集団に属していなかったと考えることが妥当なため、不満足と評価されます。
このように、z-スコアによる評価は確率に基づいており、| z-スコア | ≦ 2.0であれば正常、2.0を超えたらただちに異常というわけではありません。継続して技能試験に参加することで、z-スコアの傾向を見ることが可能になります。例えば、z-スコアが2.1であったとしても、次の回に1.0であれば全体としてはその試験所の性能は通常の範囲と考えられますが、2回連続して2.0を超えた場合、その確率は0.05×0.05=0.0025となり、性能が通常の範囲から外れている可能性が高くなります。その場合は、通常の業務のどこかに是正処置が必要であることが想定されます。
z-スコアは下式で計算されます。
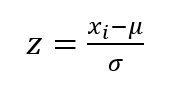 |
・・・・・式1 |
µ :参加者の報告値の平均値
σ :標準偏差 このようにz-スコアは、分布の中の位置を示すことができます。また、Fig. 1に示すように、z-スコアが −2.0から2.0の範囲には分布の95.45 %が含まれますが、z-スコアの絶対値が3.0以上になるのは0.26 %であり、分布の中では少数であることがわかります。 z-スコアに10を掛け、50を足すと、偏差値が得られます。z-スコア=1は偏差値60、z-スコア=−2.0は偏差値30となります。異なる試験結果においても、偏差値が成績の比較に使用されるのと同様に、異なる技能試験での成績の比較あるいは傾向の分析にz-スコアを用いることができます。
技能試験の報告値はz-スコアに基づいて、以下のとおり評価されます(ISO/IEC 17043: 2023 B.4およびISO 13528:2022 9.4参照)。
| | z-スコア | ≦ 2.0 | :満足 |
| 2.0 < | z-スコア | < 3.0 | :疑わしい |
| | z-スコア | ≧ 3.0 | :不満足 |
2. 平均値と標準偏差
上記でみてきたように、z-スコアの計算には、平均値 µ と標準偏差 σ の推定値が使用されます。
平均値 µ としては、技能試験参加者の平均値あるいはロバスト平均値が使用されることが一般的です。ロバスト平均値については後述します。
標準偏差 σ の決定方法は、ISO13528: 2022の箇条8に挙げられています。ISO13528は「試験所間比較による技能試験のための統計的方法」を定めた国際規格です。
性能評価規準の決定方法
・専門家の判断あるいは行政的に義務付けられた値
・前回の技能試験ラウンドからの推定
・統計的モデルから推定した値
・参加者の結果(標準偏差またはロバスト標準偏差)
・専門家の判断あるいは行政的に義務付けられた値
・前回の技能試験ラウンドからの推定
・統計的モデルから推定した値
注記 化学分析では、アナライト濃度からThompsonによるHorwitz式の修正式を用いて計算した標準偏差(次章参照)が、統計的モデルから推定した値となります。
・精度実験の結果・参加者の結果(標準偏差またはロバスト標準偏差)
3. 室間精度の予測とThompsonによるHorwitz式の修正式
室間精度の予測とは、異なる場所(室間)で同じ種類の試験や測定を行った場合に、その結果がどれだけ一貫性があるかを評価することです。同じ実験や測定を複数の場所で行ったときに、得られる結果がどれだけ近いか、ばらつきがあるかを調べることで、測定の信頼性や安定性を評価することができます。
化学分析において、分析対象濃度から室間精度を予測する式がHorwitzにより提唱され、後にThompsonにより修正されました。これをThompsonによるHorwitz式の修正式と呼んでいます。
質量分率(g/g)で表せた試験結果のロバスト平均値を c とすると、室間標準偏差は式2に従って推定されます。
なお、ThompsonによるHorwitz式の修正式はempiricalな分析(経験法あるいは定義法により行われる分析)には適用されません。
そのため、JBCO技能試験の理化学分析試験(栄養成分)では、たんぱく質、脂質、水分、灰分、炭水化物の推定標準偏差は参考値としています。
| c > 0.138 | 0.01×c0.5 | |
| 0.138 ≥ c ≥ 1.2×10-7 | 0.02×c0.8495 | ・・・・・ 式2 |
| 1.2×10-7 > c | 0.22×c |
そのため、JBCO技能試験の理化学分析試験(栄養成分)では、たんぱく質、脂質、水分、灰分、炭水化物の推定標準偏差は参考値としています。
4.ロバスト統計量(ロバスト平均値)
「1. z-スコア」で述べたように、z-スコアによる評価では、参加者の結果が正規分布していることが前提となります。しかし、参加者の結果には分布から大きく離れた値(外れ値)が含まれることがあり、このような場合に参加者の結果から平均値および標準偏差を計算すると、不適切な値が得られる場合があります。
ロバスト平均値は、統計学やデータ分析において外れ値の影響を受けにくい平均値の計算方法です。
Fig. 2に、外れ値がある場合の統計量を示します。
左側の分布は平均値10、標準偏差3とします。
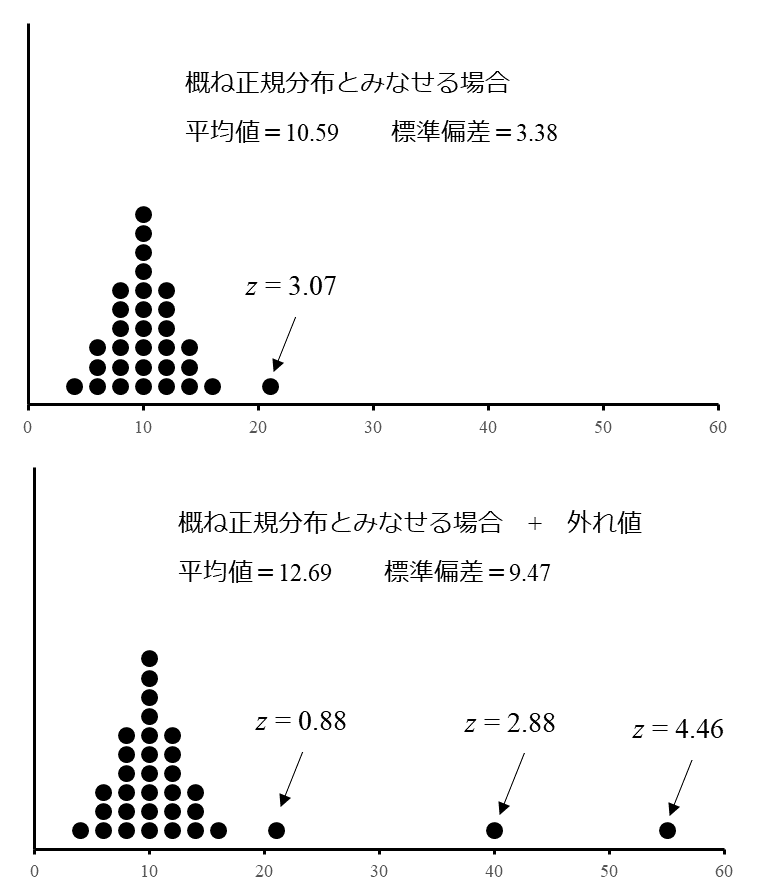 Fig. 2 外れ値がある場合の統計量
Fig. 2の上図は、少し離れた値が1個ありますが概ね正規分布となっている例です。
Fig. 2 外れ値がある場合の統計量
Fig. 2の上図は、少し離れた値が1個ありますが概ね正規分布となっている例です。
この場合、少し離れた値を含めて平均値と標準偏差を計算しても大きくは変わりません。
一方、Fig. 2の下図は、正規分布の集団に大きな外れ値が加わった例です。
この場合、大きな外れ値を含めて平均値と標準偏差を計算すると平均値、標準偏差ともに値が大きくなります。この理由として、標準偏差は特に外れ値の影響を受けやすく、外れ値があると非常に大きな値となってしまうためです。その結果、パフォーマンスが不十分な試験所が誤って満足と評価される可能性があり、適切な方法を用いて外れ値の影響を最小化する必要があります。そこで、このように大きな外れ値がある場合はロバスト統計手法を用いて計算されます。
ロバスト統計手法とは、外れ値を除去することなく外れ値以外の値の平均値と標準偏差を推定する方法であり、ロバストな統計量として
①中央値を用いる手法、
②中央絶対偏差(MADe)を用いる手法、
③正規四分位範囲(nIQR)を用いる手法、さらに
④アルゴリズムAというロバストな平均値と標準偏差を推定する手法、
があります。 平均値は分布の位置のパラメータとなりますが、外れ値があると変化しやすくなります。
それに対して、①の手法の「中央値」は外れ値の影響を受けにくい値となります。
n個の数値を昇順に並べたものを xiで表すとき、中央値は式3で示されます。
式3
②中央絶対偏差(MADe)を用いる手法の「MADe」はロバストな分布の範囲のパラメータであり、 xi の中央値をmed( x)とし、 xi とmed(x)の差の絶対値の中央値を求め、それに1.483を乗じるとMADeが得られます。
また、③正規四分位範囲(nIQR)を用いる手法の「nIQR」もロバストな分布の範囲のパラメータであり、 xi の第3四分位数(75パーセンタイル値)と第1四分位数(25パーセンタイル値)の差に0.7413を乗じた値となります。1.483および0.7413は、正規分布を想定した理論値とされています。
④のアルゴリズムAは、平均値の初期値を中央値、標準偏差の初期値をMADeとし、収束するまで以下の繰り返し計算を行ってロバストな平均値と標準偏差を得る手法となります。 平均値の推定値(はじめは初期値)を x *、標準偏差の推定値を(はじめは初期値)s*とします。
δ=1.5s* とし、
xi< x*– δ の時は xi*= x*– δ
xi< x*+ δ の時は xi*= x*+ δ
それ以外は xi*=xi とします。

この場合、少し離れた値を含めて平均値と標準偏差を計算しても大きくは変わりません。
一方、Fig. 2の下図は、正規分布の集団に大きな外れ値が加わった例です。
この場合、大きな外れ値を含めて平均値と標準偏差を計算すると平均値、標準偏差ともに値が大きくなります。この理由として、標準偏差は特に外れ値の影響を受けやすく、外れ値があると非常に大きな値となってしまうためです。その結果、パフォーマンスが不十分な試験所が誤って満足と評価される可能性があり、適切な方法を用いて外れ値の影響を最小化する必要があります。そこで、このように大きな外れ値がある場合はロバスト統計手法を用いて計算されます。
ロバスト統計手法とは、外れ値を除去することなく外れ値以外の値の平均値と標準偏差を推定する方法であり、ロバストな統計量として
①中央値を用いる手法、
②中央絶対偏差(MADe)を用いる手法、
③正規四分位範囲(nIQR)を用いる手法、さらに
④アルゴリズムAというロバストな平均値と標準偏差を推定する手法、
があります。 平均値は分布の位置のパラメータとなりますが、外れ値があると変化しやすくなります。
それに対して、①の手法の「中央値」は外れ値の影響を受けにくい値となります。
n個の数値を昇順に並べたものを xiで表すとき、中央値は式3で示されます。
式3
| nが奇数の時 | 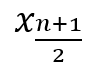 |
| nが偶数の時 | 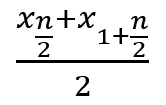 |
また、③正規四分位範囲(nIQR)を用いる手法の「nIQR」もロバストな分布の範囲のパラメータであり、 xi の第3四分位数(75パーセンタイル値)と第1四分位数(25パーセンタイル値)の差に0.7413を乗じた値となります。1.483および0.7413は、正規分布を想定した理論値とされています。
④のアルゴリズムAは、平均値の初期値を中央値、標準偏差の初期値をMADeとし、収束するまで以下の繰り返し計算を行ってロバストな平均値と標準偏差を得る手法となります。 平均値の推定値(はじめは初期値)を x *、標準偏差の推定値を(はじめは初期値)s*とします。
δ=1.5s* とし、
xi< x*– δ の時は xi*= x*– δ
xi< x*+ δ の時は xi*= x*+ δ
それ以外は xi*=xi とします。
この操作で、 x* から1.5s*以上離れた値は、 xi*= x*– δ または xi*= x*+ δ になるので、大きく離れた値があってもその値の影響はなくなります。
変換したxi*の平均値と標準偏差を通常の方法で計算し、平均値を新たな x* 、標準偏差×1.134 を新たな s* とします。
以上の操作を x* と s* の有効数字3桁目が変化しなくなるまでくり返し、その時の x* をロバスト平均値、 s* をロバスト標準偏差とする手法です。
変換したxi*の平均値と標準偏差を通常の方法で計算し、平均値を新たな x* 、
以上の操作を x* と s* の有効数字3桁目が変化しなくなるまでくり返し、その時の x* をロバスト平均値、 s* をロバスト標準偏差とする手法です。
以上
